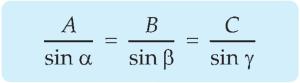Metode Penjumlahan Vektor
Dua buah vektor atau lebih dapat dijumlahkan. Hasil penjumlahan tersebut disebut vektor resultan.
a. Penjumlahan Vektor dengan Metode Grafis (Poligon)
Sebagai contoh suatu vektor A ditambah dengan suatu vektor B maka vektor resultannya VR
Langkah-langkah penjumlahan vektor secara grafis (metode poligon) adalah sebagai berikut:
1. Gambar vektor A sesuai dengan skala dan arahnya
2. Gambar vektor B sesuai dengan skala dan arahnya dengan menempelkan pangkal vektor B pada ujung vektor A .
Gambar 1.4. Penjumlahan dua buah vektor A dan B dengan metode grafis (poligon)
Gambar 1.5. Penjumlahan empat buah vektor A, B, C dan D secara grafis (metode poligon) VR = A + B + C + D
Penjumlahan dengan metode poligon maka vektor resultan VR adalah segmen garis berarah dari pangkal vektor A ke ujung vektor B yang menyatakan hasil penjumlahan vektor A dan B .
b. Penjumlahan Vektor dengan Metode Jajaran Genjang
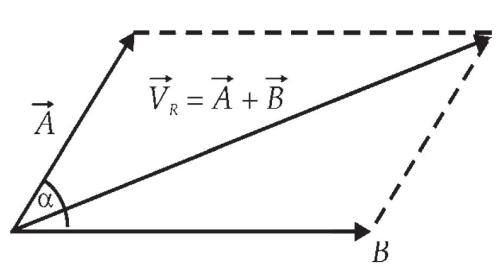
Penjumlahan dua buah vektor A dan B dengan metode jajar genjang yaitu dengan cara menyatukan pangkal kedua vektor A dan B , kemudian dari titik ujung vektor A ditarik garis sejajar dengan vektor B dan juga dari titik ujung vektor A ditarik garis sejajar dengan vektor B . Vektor resultan VR diperoleh dengan menghubungkan titik pangkal ke titik perpotongan kedua garis sejajar tersebut di atas.
Gambar 1.6 Penjumlahan dua buah vektor A dan B dengan metode jajar genjang.
Besar vektor resultan VR yang ditunjukkan pada Gambar 1.6. di atas dapat dicari dengan persamaan cosinus berikut ini:
dengan VR = besar vektor resultan,
A dan B = besar vektor A dan B ,
α = sudut antara vektor A dan B .
A dan B = besar vektor A dan B ,
α = sudut antara vektor A dan B .
Arah vektor resultan terhadap salah satu vektor secara matematis dapat ditentukan dengan menggunakan aturan sinus. Contoh suatu vektor A ditambah vektor B dan hasil penjumlahan ini adalah vektor C.
dengan α, β, γ merupakan sudut-sudut yang terbentuk antara dua vektor seperti gambar 1.7.
Gambar 1.7 Penjumlahan dua vektor A dan B menjadi vektor C.
Jika vektor A dan vektor B saling tegak lurus maka besar vektor penjumlahannya C = A + B dapat ditentukan dengan dalil Phytagoras yaitu:
Gambar 1.8 Penjumlahan dua vektor yang saling tegak lurus.
dengan :
A = besar vektor A,
B = besar vektor B,
C = besar vektor C.
A = besar vektor A,
B = besar vektor B,
C = besar vektor C.
Read more: http://fisika-bse.blogspot.com/2013/05/metode-penjumlahan-vektor.html#ixzz2dzdtkFPt